四環(huán)凍干機—真空冷凍干燥傳熱傳質(zhì)原理（五）
發(fā)布時間:2023-12-271次瀏覽
2.2.2多孔介質(zhì)的凍干理論
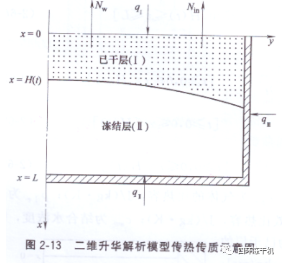
1979年利亞皮斯(Liapis))和利奇菲爾德(Litchfield）等提出了冷凍干燥過程的升華-解析模型。該模型的思想是把已干層當(dāng)做多孔介質(zhì)，利用多孔介質(zhì)內(nèi)熱質(zhì)傳遞理論建立已干層內(nèi)的熱質(zhì)傳遞模型。該模型的特點是：簡化條件相對來說比較少，能較好地模擬凍干過程，與實際情況比較接近，但求解較困難，所需物性參數(shù)較多。近年來有不少學(xué)者在此基礎(chǔ)又做了進一步改進，多數(shù)是為了提高藥品的質(zhì)量和干燥速率而建的模型。
2.2.2.1一維升華-解析模型
一維升華-解析模型 (1979 年 Liapis 和 Litchfield 提出的)，在主干燥過程傳熱傳質(zhì)的物理模型如圖2-12所示。已干區(qū)(I)和凍結(jié)區(qū)(II)非穩(wěn)態(tài)能量傳熱平衡方程為：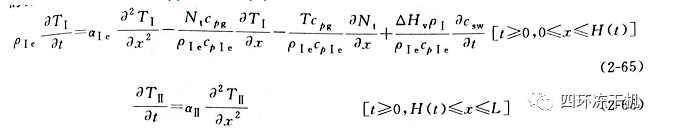
傳質(zhì)連續(xù)方程為：
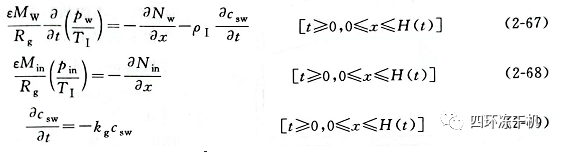
式中，N_t為總的質(zhì)量流,kg/(m²?s) ；C_pg為氣體的比熱容，J/(kg?K)；ρ_Ie為已干層的有效密度，kg/m³; c_pIe為已干層有效比熱容，J/(kg·K)；c_sw為結(jié)合水濃度，kg水/kg固體；ρ_I為已干層密度，kg/m³ ；ε為已干層的孔隙率(無量綱)；M_w為水蒸氣分子量，kg/mol；R_g為理想氣體常數(shù)，J/(mol·K)；p_w為水蒸氣分壓，Pa；N_w為水蒸氣質(zhì)量流，kg/(m²·s)；M_in為惰性氣體分子量，kg/mol； N_in為惰性氣體質(zhì)量流，kg/(m²?s)；p_in為惰性氣體分壓，Pa；κ_g為解析過程的內(nèi)部傳質(zhì)系數(shù)，s^-1； H(t)為t時刻移動冰界面的尺寸，m；△H_v為結(jié)合水解吸潛熱，J/kg。
該模型適合于可簡化成平板狀的物料，例如牛奶的凍干。

2.2.2.2二維軸對稱升華-解析模型
二維軸對稱解析升華模型( 1997 年Mascarenhas等人提出的) ，在主干燥過程傳熱傳質(zhì)的物理模型如圖2-12所示。
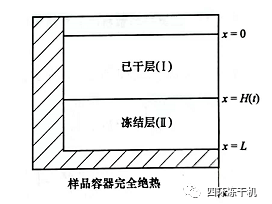
已干區(qū)(I)和凍結(jié)區(qū)(Ⅱ)非穩(wěn)態(tài)傳熱能量平衡方程為：
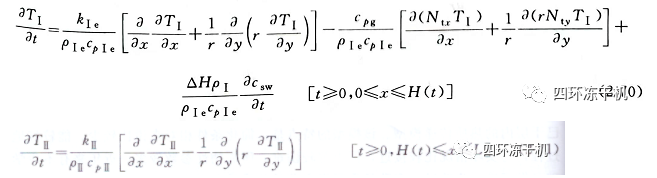
傳質(zhì)連續(xù)方程為：
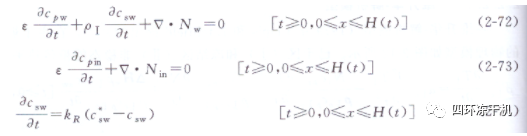
式中,κ_I_e 為已干層有效熱導(dǎo)率，W/ (K?m)；k_Ⅱ為凍結(jié)層熱導(dǎo)率，W/(K?m)；C_pw為水蒸氣的質(zhì)量濃度，kg/m³；c_p_in為惰性氣體的質(zhì)量濃度，kg/m³；c^*_sw為結(jié)合水平衡濃度，kg水/kg固體；N_tx為x方向總的質(zhì)量流，kg/(m²?s)；N_ty為y方向總的質(zhì)量流，kg/(m²·s)；其余符號同前。
圖中 2-13 中 q_Ⅰ、q_Ⅱ和q_Ⅲ為來自不同方向的熱流,W/m²。
2.2.2.3多維動態(tài)模型
實際為二維軸對稱模型(1998年Shee- han和Liapis提出的)，干燥過程傳熱傳質(zhì)物理模型可簡化成如圖2-14所示。主干燥階段在已干層和凍結(jié)層中傳熱能量平衡方程為: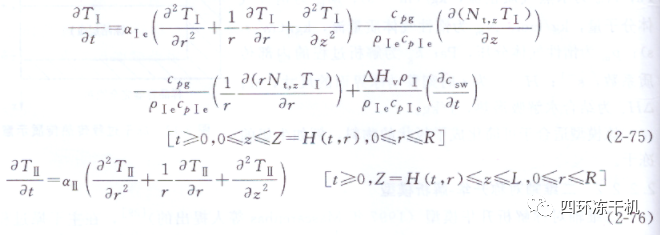
傳質(zhì)連續(xù)方程為：
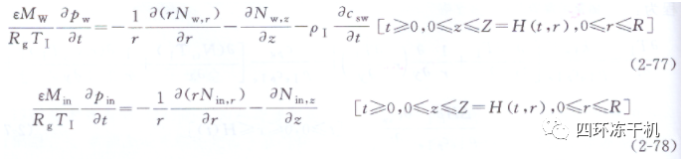
二次干燥階段傳熱傳質(zhì)平衡方程為:
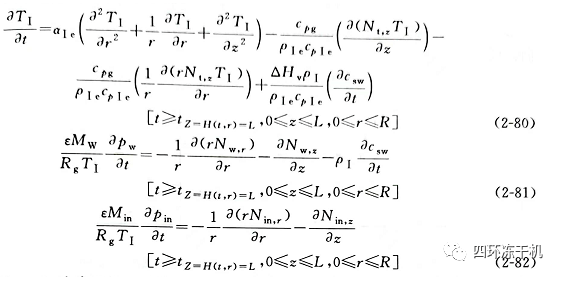
式中，H(t, r)為半徑為r時的H(t); Z為移動冰界面到達z處的值；N_t,z為z方向總的質(zhì)量流，kg/(m²· s)；N_w,r和N_w，z分別為r和z方向水蒸氣的質(zhì)量流，kg/(m²· s)；N_in，r和N_in_,z分為r和z方向惰性氣體的質(zhì)量流，kg/ (m²·s)；其余符號同前。
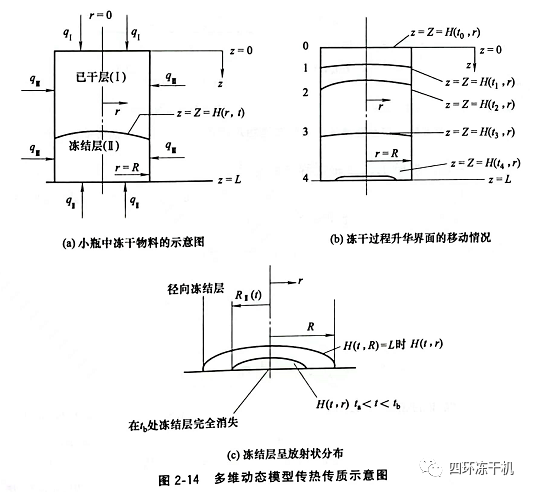
上述模型只是對于單個小瓶來說，如果對排列在擱板上的多個小瓶來說，可以認(rèn)為對小瓶的供熱是排列位置的函數(shù)，同樣可以使用。該模型的優(yōu)點是能提供小瓶中已干層中結(jié)合水的濃度和溫度的的濃度和溫度的動力學(xué)行為的定量分布。

2.2.2.4考慮瓶塞和
考慮瓶塞和室壁溫度影響的二維軸對稱非穩(wěn)態(tài)模型的物理模型如圖2-15所示。數(shù)學(xué)模型與1998年Sheehan和Laps提出的多維動態(tài)模型相同，即與式（2-75)～式(2-82)相同，只是確定邊界條件qⅠ、9Ⅱ、9Ⅲ時考慮了瓶塞和干燥室壁溫度的影響。

2.2.2.5考慮平底彎曲影響的二維軸對稱非穩(wěn)態(tài)模型
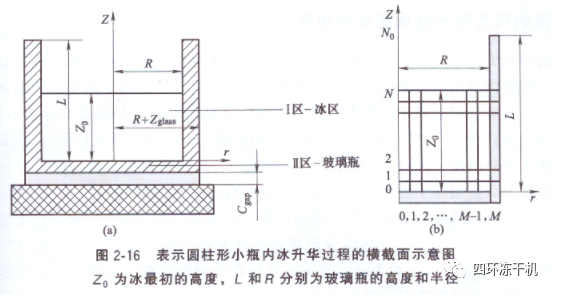
2005年Suling Zhai等提出的考慮平底彎曲影響的二維軸對稱非穩(wěn)態(tài)模型的物理模型如圖2-16所示。主干燥階段傳熱能量平衡方程為
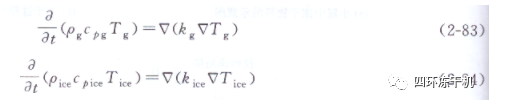
傳質(zhì)連續(xù)方程為
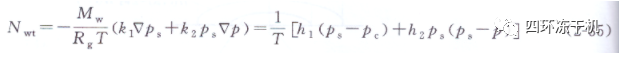
式中，ρ_g為玻璃瓶的密度，kg/m³,c_pg為玻璃瓶的比熱容，J/(kg·K)；T_g為玻璃瓶的溫度，K；k_g為玻璃瓶的熱導(dǎo)率，W/(K·m),ρ_ice為冰的密度，kg/m³,c_pice為冰的比熱容，J/(kg·K)，T_ice為冰的溫度，K；k_ice為冰的熱導(dǎo)率，W/(K·m)；M_w為水蒸氣分子量，kg/mol；R_g為理想氣體常數(shù)，J/(mol·K)；p_s和p_c分別表示升華界面和冷凝器表面標(biāo)準(zhǔn)水蒸氣壓力，Pa；p為千燥室的內(nèi)總壓力，Pa；Nwt為水蒸氣總的質(zhì)量流，kg(m²·s)；k₁和k₂分別為體擴散和自擴散常數(shù)；h₁和h₂分別為擴散和對流傳質(zhì)系數(shù)，m/s。
圖2-16中,C_gap為玻璃瓶底的彎曲孔隙的高度，mm。

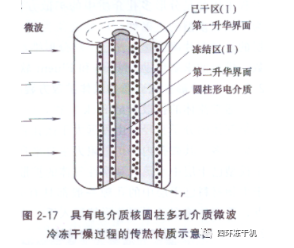
2.2.2.6微波凍干一維圓柱坐標(biāo)下的雙升華面模型
圖2-17為簡化的具有電介質(zhì)核圓柱多孔介質(zhì)微波冷凍干燥的雙升華界面模型的一維圓柱坐標(biāo)物理模型。對具有電介質(zhì)核的多孔介質(zhì)微波冷凍干燥過程，物料將被內(nèi)外同時加熱，因而可能產(chǎn)生2個升華界面。一方面，物料外層的冰吸收微波能而升華，形成第一升華界面；另一方面，由于電介質(zhì)核較冰的損耗系數(shù)大，微波能主要被其吸收并傳導(dǎo)至物料層使冰升華, 從而形成第二升華界面。因此, 多孔介質(zhì)內(nèi)部將出現(xiàn)2個干區(qū)、冰區(qū)和電介質(zhì)核4 個區(qū)域 (見圖2-17)。
已干區(qū)傳熱能量平衡方程:
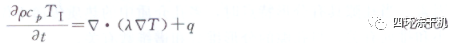
傳質(zhì)連續(xù)方程：
凍結(jié)區(qū)傳熱能量平衡方程：
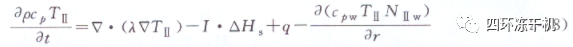
傳質(zhì)連續(xù)方程：
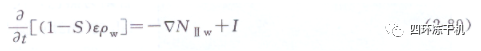
式中,λ為熱導(dǎo)率，W/(m?K)；I升華源強度，(kg·m³)/s；△H_s為升華潛熱，J /kg；q為微波能吸收強度，J/(s·m³)，S為飽和度；其余符號同前。
上一個：四環(huán)凍干機—真空冷凍干燥傳熱傳質(zhì)原理（四）

下一個：四環(huán)凍干機—真空冷凍干燥傳熱傳質(zhì)原理（六）